以前IkaLogの開発で得た知見:大量の動画や画像を取り扱う際の Tips にて、 IkaLog が使用していたブキ認識において、いかに実ユーザ環境からの送信データを活用しながらいかに効率的に教師データを揃えることができたかを紹介しました。
最近は LLM や生成 AI などが話題をもっていきがちですが、独自のモデルを構築してアプリケーションに組み込もうというアイデアで取り組まれている方も増えているのではないでしょうか。
私自身が取り組んだのは 2015-2017年頭の話なので昔話でしかないとはいえ、もしかしたら新規アプリケーションを作られる方の参考になるかもしれない?と思ったので、当時どのような思考で作業をしていたか、もう少しまとめてみる事にしました。
今回は、 IkaLog のブキ認識において、最終的にシンプルなニューラルネットワークに行きついたかについて解説します。
バックグラウンド: IkaLog で目指した性能と、当時のハードウェア制約
精度99%では満足できなかった理由
スプラトゥーンでは、合計8名のプレイヤーがふたつのチームに分かれて勝敗を競います。このときひとりひとりのプレイヤーが100クラス以上のブキのなかからひとつ選んで勝負に挑みます。
ブキにはそれぞれシューター/ローラー/ブラスターなどのクラスの特徴があるほか、攻撃力や距離、連射力で差別化がされています。また、ブキには戦局を有利に進めたり、不利な場面を打開するために活用できるサブウェポンやスペシャルウェポンが用意されています。
IkaLog で処理される勝敗データでは、各プレイヤーがどのメインブキを使用しているか、またサブウェポンやスペシャルウェポンが何であるかを正しく記録することが、戦績データを扱うためのしくみとして重要だと考えていました。
※ この統計自体には IkaLog は使われていません
先述のとおり、一回の対戦において8名のプレイヤーがゲームに参加します。これは 99% の分類器があったとしても、対戦で使われたブキすべてが正しく分類できる確率は 0.99^8 = 92.2% にしかなりません。このため IkaLog ではブキ分類器で 99.9% 以上の精度が必要であろうと考えていました。
スプラトゥーンのリザルト画面からのブキ認識は今のAIの仕組みから考えれば、とても簡単な仕組みです。画面の同じ場所に同じ画像が表示されるだけ。ただ、バグありのビデオキャプチャデバイス、HDMIでさりげなく入るノイズ、ユーザーのセットアップなどの理由で、ソフトウェア観点からみると「同じ画像が毎回表示される」前提ではブキ分類器を実現できませんでした。
当時のハードウェア事情
また、 IkaLog を開発していた 2015 年頃はまだゲーミングPCらしくゲーミングPCを一般的なプレイヤー層は持っていることは想定できませんでした。
ましてや Wii U でスプラトゥーンをプレイしているユーザがとなりに AI で十分な性能を発揮できるようなハードウェアを持っておらず、ゲームをしている人が最新CPU搭載のコンピュータを所有しているかも怪しいです(今でも多くのスプラトゥーンプレイヤーでも余裕のあるPCを持っておらず、むしろスマホのほうが性能が高い可能性すらあるでしょう)。当時の事情でいえば、x86 CPUでの演算において SSE4.2 程度の命令セットしか期待できなかった時期での取り組みでした。私自身が認識できていたユーザには Core 2 Duo で IkaLog を常用している方もいらっしゃいました。
IkaLog がリアルタイムで画像認識をするというコンセプトであったため、当時の記録によると、8キャラクタ分のブキ分類を含めてリザルト画面の解析をおよそ3秒以内で実現できることをひとつの目安としていたようです。
IkaLogの開発においてたどった当初の分類器のしくみや遷移
K近傍法
IkaLog では、当初は OpenCV の K近傍法 の実装を用いて、入力画像に対してもっとも特徴量ベクトルが近い近傍があるクラスに分類するアプローチで実装していました。
開発開始当初はブキ数が30程度だったかと思いますが、アップデート終了までにクラス数が100を超えるほどに増えました。結果論ですが、単純なテンプレートマッチングやSVMなどといったアプローチをとっていたら、実行時間の観点から、より苦労していたと思います(スプラトゥーン2向けの実装では数字などのキャラクタ認識でSVMを利用することも検討し取り組みましたが、このワークロードではKNNほどコスパよくありませんでした)。
KNN の実装は当時の CPU でアイコン程度を分類するのは十分に高速だったほか、分類器の訓練も高速でしたので、開発初期からこのアプローチにたどり着いていたことはとても助かりました。データ量が少ない状態から半自動的に訓練データを集めようとしたときに、いまでもとりあえず使うことが多いです。
色相のヒストグラム
ブキの分類器を作り始めた当初、最初に実装したものは色相のヒストグラムからパターンを見つけて分類が可能かどうかを試していました。
ただ、スプラトゥーンのリザルト画面では、所属チームによりブキ画像の背景にチーム色が映り込み、場合によってはプレイヤーが選んだ装備品もブキに重なります。プレイヤーのキャプチャーデバイスの設定などにも依存することもあり、あまり実用的な精度は出せませんでした。
ラプラシアンフィルタ輪郭抽出は古典的な画像の分類アプローチでよく使われる手法の一つかと思います。IkaLogでもラプラシアンフィルタを適用し、カラー画像から次元数を削減した特徴量を生成し、ここから分類を行う方法を試していました。一時期のバージョンの IkaLog では実際にこのアプローチで提供していたと思います。
IkaLogのブキ分類のワークロードにおいてラプラシアンフィルタはチームの背景色の影響を排除し、ブキの形状に基づいて分類するには良い方法に思えます。しかし、ユーザの映像キャプチャ環境において元画像が 720/1080p だったり、それを480pにリスケールした映像が投入されたりといったかたちで想定外の入力がされると精度を保てないという問題が生じました。
最終的なチャレンジはスプラトゥーンのアップデートそのものでも発生しました。スプラトゥーンではメインブキに対して、サブウェポン・スペシャルウェポン違いのバージョンとして「カスタム」「コラボ」といった亜種が登場します。これらの亜種ではブキ画像の右下に小さな追加マークが表示されるのですが、ラプラシアンフィルタを介して色相情報を落とした状態でこれらの特徴を合理的に見分けることはできませんでした。
ニューラルネットワーク導入の決断
IkaLog を作り始めて自然と機械学習的アプローチに関わるようになっていたことから、 Cousera の Andrew Ng 先生のコースなども一通り修了していた頃に「もうニューラルネットワークにカラー画像をそのまま入力したほうがいいんじゃないか」考えるようになってきていました。
とはいえ、AlexNet などの既存のニューラルネットワークは100MB以上の重みデータがありますが、さすがにこれは過剰ですし、ユーザがそんなもので推論できるようなプロセッサを持っていませんし、CUDAをユーザのプロセッサで実行できるわけでもありません。このため IkaLog で目的に合わせたニューラルネットワークを実装することを考え始めました。
IkaLog のブキ分類においてニューラルネットワークに画像をそのまま入力することによる一つのメリットは、ニューラルネットワークであれば背景色などを無視できることがあります。チームカラーによって何色になるかわからないようなピクセルに基づく入力値は、結果的に無視されるようになります。ブキの形状によって適切な重みが自動的に形成されることを想定できたので、おそらく簡単にうまくいくだろうと思いました。
HSV色空間
RGBとHSVでしっかり比較したわけではないのですが、ブキ分類器での分類対象ではHSV色空間で取り扱ったほうがよいだろうと判断したので、何も考えずにHSV色空間を特徴量として使用しています。
HSV色空間を利用しようと思った最大の理由は、ブキの「カスタム」「コラボ」といった亜種の特徴を表現する色相がピクセルあたりひとつのパラメータで表現されることになるので、おそらくRGB色空間で扱われるよりもいいだろう、ぐらいにしか考えていませんでした。背景の色相を無視するという観点でも重みが小さくなることで簡単に表現できるでしょう。ここについては「こうなってくれたらいいな」という思想でしかなくて、現時点でもそう思っているだけで、これによる差があったかどうかは何も検証していません。
ネットワーク構成をシンプルに
使用するレイヤとしては単純な全結合とReLUに制約することにしました。理由はふたつあり、一つ目は計算量、二つ目は再実装のしやすさです。
計算量の観点では、畳み込みフィルタなども考えましたが、当時 MacBook Pro (2014) とその上の GeForce チップ、また Haswell Refresh プロセッサで走るニューラルネットワークの速度を見ていると、 CNN やプーリングをエンドユーザのプロセッサで実行させることは現実的ではないだろうと感じていました。単純な全結合と ReLU 程度であれば、当時で型落ちとなっていたプロセッサ上でも NumPy やその下位のライブラリが現実的なスピードで動いてくれるだろうと期待しました。
再実装の観点では IkaLog に取り組んでいた当時でニューラルネットワークを動かそうと思うと、 Caffe を使うとか、もしくは Chainer を使うとか、そういったいくつかのフレームワークを利用する方法でした。 ONNX ランタイムみたいなものはまだ出てきておらず、想定するユーザ層が中学生・高校生・大学生や社会人で、主に Windows ユーザであろうことを考えると、既存のフレームワークを IkaLog のためにセットアップさせるのは不可能でしょう。
IkaLog は zip ファイルを展開して実行すれば使える状態の配布形態を維持することを心がけていたので、ブキの分類器のためにフレームワークへ依存を追加することにためらいました。このため、シンプルなネットワーク構成とすることで、IkaLog用に推論コードを作成するコストを最低限に抑えることにしました。
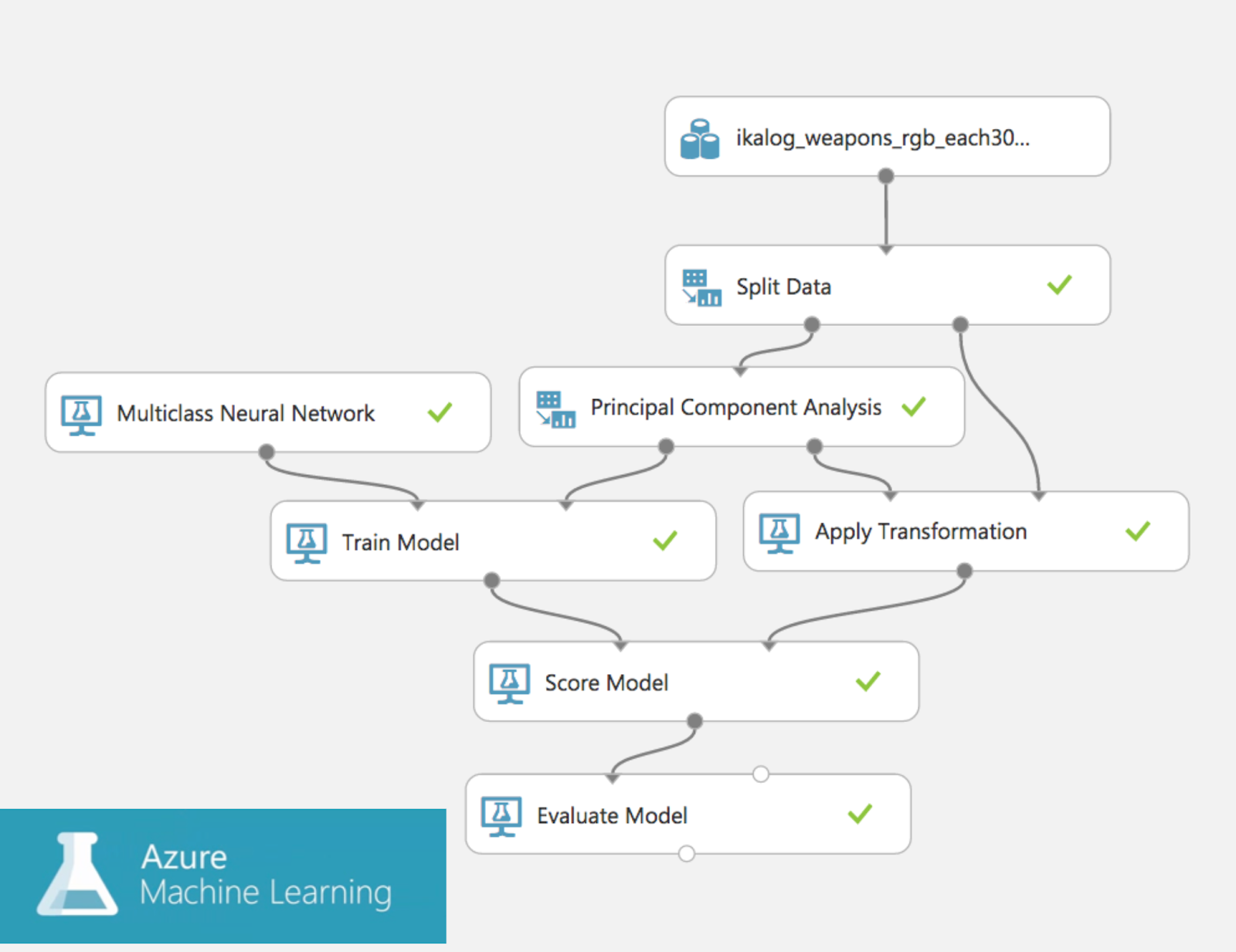
実装を進める前の事前確認を Azure Machine Learning で実行
それまでの取り組みである程度のデータ量は確保できていたので、まずは手元のデータセットを用いて最低限の作業でアプローチを検証するため、 Azure Machine Learning に想定する特徴量をアップロードして、 MLPで期待するようなモデルが実現するのかを確認しました。
Azure ML はこの程度のワークロードであればファイルをアップロードしポチポチするだけでいいですし、 confusion matrix などもさくっと出してくれるので、アプローチ上問題がないことを簡単に確認できましたしコードを具体的に書く前に最低限の労力で検証できたことはとても助かりました。なおこの Azure ML の体験談は 2016 年頃当時の話であることに留意してください。
学習済みモデルのインポート、推論
実際の学習は Chainer と GeForce GTX 1080 (後半は Tesla P100)で行いました。そもそもどれぐらいのノード数で性能が飽和するかを Chainer 上で検証し、ネットワークの隠れ層のサイズを決めました。
本番の学習は 24 時間などのオーダーで1000エポック以上回したような覚えがあります。 Chainer のチェックポイントとして得られたものをいくつか評価して使用するモデルをきめました。

Chainer フレームワークからネットワークの重み・バイアスを取り出して、単純な NumPy コード上で推論できることを確認できたので、モデルをただのマトリックスとして pickle してファイルに保存、そこからモデルを復元・推論することで、機械学習フレームワークへの依存を断ち切りました。
実際に生成できた実行用モデルファイルをみてみると15MBほどになっていました。この中には32ビット浮動小数点数が並んでおり、zipなどでの圧縮効果がほとんどありません。配布ファイルが大きくなることを嫌って、pickcleする際に16ビット浮動小数点数として扱うことによってファイルサイズを半分に抑えることにしました。このワークロードとモデルにおいて浮動小数点数のビット数を抑えても実用上の影響はほとんど感じられません。最終的に戦績共有サイト stat.ink に投稿されるブキ画像を 99.99% で分類できる精度が得られました。
推論の実装
先述の理由で、 IkaLog ではフルスクラッチかつ最低限のコード量で推論を再実装しました。ここで実装した内容は、のちに発売されるオライリーの「ゼロから作る Deep Learning」の最初の100ページで解説された内容そのものともいえるかと思います。
このブキ分類器は、すでに型落ちとなっていた IvyBridge 2.0 の MacBook Air でも 0.02 秒で実行できました。Core 2 Duo などでも十分な速度で動きましたし、 PYNQ (ARMコア搭載 FPGA)でも1回あたり200ms未満の実行速度で収まりました。
FPGAならPLで実行すりゃもっといけるだろとかそういうツッコミはいくらでも可能かと思いますが、技術的には可能ですが、非営利の独りプロジェクトでここまでやれば十分かなと思っています。
おまけ
当時やってみたかったこと
ネットワークの蒸留や枝切りをしてより配布ファイルのサイズを小さくできるのではないかと考えていましたが、着手しませんでした。
単に手が回っていなかったほか、ネットワークの規模が小さくなったときに、どのクラスにも該当しない画像を特定のクラスに分類してしまう可能性などを恐れていたように思います(実際取り組んだらどうなったかはわかっていません)。
最近のエコシステムに思うこと
ここまでの内容を2017年以前に取り組んだ後、こんなフレームワーク便利だなと思ったものが幾つかでてきました(現時点の選択肢として筋がいいと言いたいわけではありません)。
- ONNX Runtime の登場によりホストプログラムが雑に使える推論ライブラリが出てきたという印象
- Intel が OpenVINO や Movidius VPU を出してきて、 Windows PC でハードウェア支援が期待できるようになった。最悪 AMD CPU でも SSE 相当で動くっぽい
- OpenCV に DNN に対する推論機能が強化されており、配布方法を工夫すれば GPU アクセラレーションなどをホストプログラムから呼び出せるかもしれない。
さらに、2017年の iPhone X から Neural Engine が搭載され、 Android にも同じように推論エンジンがハードウェアとして搭載されるようになりました。 Mac であれば M1 から、 Windows でも Copilot PC が出てきました。
ようやく OS レベルの推論の抽象化が進んできた
ライブラリの観点では、Windows であれば DirectML 、 Apple であれば CoreML 、Androidであれば MLKit などが普通に使えるようになってきて、私が IkaLog を作るときに困った「推論のための仕組みがない。ターゲットごとに実装してられない」という状況に大きな変化が起きているように感じています。特に個人的には DirectML は(ごくたまにしか試してませんが) Windows 環境において OS が推論ワークロードをハードウェアで実行してくれるという、まさに OS らしい抽象化をしてくれるようになりました。
私自身はふだんほとんどプログラムを書かないのですが、ローカルで推論をするアプリケーションの開発難易度は10年前から比べると大きく下がってきたなと感じています。
ローカル LLM の話題などもみかけますが、 Copilot PC の話題などをみつつ 2024 年は、ローカルで推論をするタイプのアプリケーションの開発が加速する年になるだろうなと思っています。2025 年になるとウイルス対策ソフトすら推論用アクセラレータにオフロードするような世界がくるのかもしれませんね。